数学を美しいと感じますか？
シンプルな式の中に隠された解が、整然としたものであったときに、僕は美しさを感じます。
　またシンプルで無駄の無い公式は、贅肉を削ぎ落としただけのように見えますが、実はふところに多くの事柄を内包していると思ってます。たとえばオイラーの定理(※1)やアインシュタインのエネルギー・質量保存則(※2)などは美しく奥深い式の最たるものです。

　僕が物理学科を選んだのも、理論物理の美しさへの憧れがあったのだと思います。
もし神がこの世をお創りなったのなら、この世はきっと美しくシンプルであることでしょう。宇宙の始まりも原子の組成にもシンプルな美しさが潜んでる気がします。

　もし別の宇宙があったとすると、物理や化学の法則すら成り立たないことも考えられます。しかし、唯一数学だけはどんな場合でも成り立つ学問です。例えば宇宙人や異次元人とコンタクトする時でも数学だけは通用します。

　有名な「フェルマーの最終定理」(※3)を解くためにアンドリュー＝ワイルズは「谷山＝志村予想(定理)」(※4)の一部を証明しました。　「フェルマーの定理」を証明したことも価値のあることですが、「谷山＝志村定理」の証明は「フェルマーの定理」よりはるかに意味のあることです。　谷山＝志村定理(モジュラー性定理)は、数学界の異分野の架け橋となり、「数学の大統一」の鍵となる理論だということです。
　物理学の「力の超大統一理論」も遠い道のりですが、構築されつつあります。

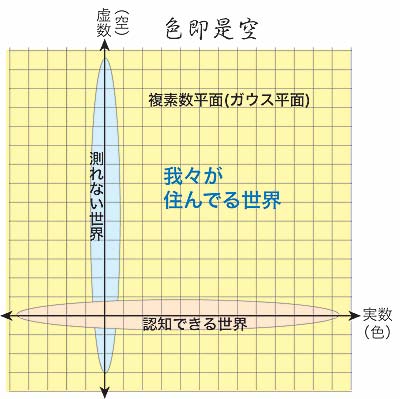
　普段、我々は実数だけを意識して暮らしていますが、実は虚数も含めた複素数(※6)が同じ世界を構成してるのでは？
　我々と書きましたが、人間だけじゃなくって、動物や植物、さらには鉱物や分子・原子までもが、人間と同様に実軸に位置しています。　ということは「森羅万象すべての物体に、それぞれ固有の虚数部分がある」ということです。

　虚数部分は、例えば「神」や「悪魔」、「魂」や「祈り」、「意識」「スピリッツ」「オーラ」「超能力」、さらに「運」「陰徳」「感謝の気持ち」など。　目に見えないし、あるかないかもわからない、物事の動きに直接的に関係無さげな部分です。

　　　　　　　　　　　　　　　　　　　　　　　　

　グラフの横軸(実軸)は我々が普通に認知できる世界です。

ある事象が 3+3i だったものが 7+3i になれば、 4 upしたことになります(青い矢印)。

これが 3+3i が 3+9i になったとしても、外観上は何の変化もありません(赤い矢印)、しかし虚数部分は明らかに変化しています。
　虚数であるから　たとえば 3i と 9i には普通の意味での大小は存在しません。でも、移動距離( 6i )だけ、なにかが確実に変わったのです。

青の矢印は、自分の行動や他人への働きかけで変わります。
では、赤の矢印はどうやったら変化するのでしょうか？

　具体的な働きかけができないのであれば、先述の「目に見えないし、有るか無いかもわからない」チカラを使うしか無さそうです。

「色即是空　空即是色」は宇宙の真理というものを端的に言い表しているんでしょう。

数学と宗教いやもとい数学と現世とは繋がっていた。

※6;複素数
　実数と虚数を用いて a + bi で表せる数